2025年6月10日
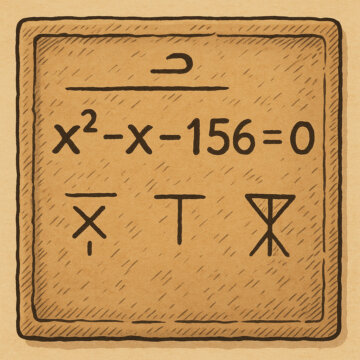
「4000年の歴史をもつ2次方程式」
ねえ、みんな。
突然だけど、「2次方程式」って聞いたことあるかな? たぶん授業で出てきたよね。
でも、それが 4000年も前から使われてた って知ってた?
ちょっと驚くかもしれないけど、本当の話なんだ。
「足して9、かけて20になる2つの数」って?
では、まず簡単な問題を出してみるよ。
「足して9、かけて20になる2つの数って何かな?」
……うんうん、ゆっくりでいいよ。
答えは「4と5」だね。4+5=9、4×5=20。
この問題を、ちょっと数学っぽく書いてみると…
x² – 9x + 20 = 0
これが、2次方程式ってやつなんだ。
図形として見ると、こんなイメージ
さて、ここでちょっと視点を変えてみよう。
式って、数字や文字の並びに見えるけど、実は図形として考えると意外とわかりやすいんだよ。
たとえば
- x² → 正方形の面積(1辺がx)
- bx → 縦と横が違う長方形の面積
- c → 固定された大きさの面積、ちょっとしたパーツみたいなもの
こうやって考えると、「式をゼロにする」っていうのは、図形のパズルを組み立てて、ぴったり全部合わせるって感じかな。
ちょっと面白くない?
え、2次方程式ってそんなに昔から?
そう、実は解いてたんだよ。
古代メソポタミアの時代――つまり、今から4000年も前の話。
その頃の人たちが書いた粘土板に、こんな問題が残ってるんだ。
「正方形の面積から、その1辺の長さを引いたら156だった。その1辺を求めよ。」
ちょっと現代風に式にしてみると
x² – x = 156
整理すると
x² – x – 156 = 0
もう見慣れた2次方程式の形だね。
ちょっとやってみようか?
公式に当てはめてみようか。
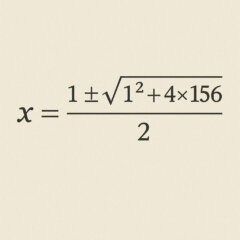
……計算できた?
答えは、13と-12。
でも、1辺の長さを求める問題だから、正の数の13が正解になるよ。
式は道具、でも物語もある
2次方程式って、最初は「ただの式」って思うかもしれない。
でも、そこには人が考えてきた歴史とか、工夫とか、ちゃんと詰まってるんだよね。
なんか、「公式を覚えるため」だけじゃなくて、自分もその知恵の流れに乗ってるんだって思うと、ちょっといい感じじゃない?
